

The COBRAme Web App aims to bring the power of Metabolism and Expression (ME) modeling to the wider scientific community. Our goal is to make it easier for researchers to run, explore, and interpret complex ME models without needing extensive programming expertise.
Modern biology seeks to predict how cells behave under diverse conditions, and the most powerful tools we have for this are genome-scale models (GEMs), which are computational frameworks that simulate all known biochemical reactions inside a cell. Over the past two decades, these models have grown from focusing solely on metabolism (M-models) to also incorporating gene expression machinery, such as transcription and translation. This expansion has led to the development of ME-models.
ME-models are a major step forward in realism. Unlike earlier metabolic models that assume enzymes are freely available, ME-models explicitly account for the cost of producing the enzymes themselves. That means they simulate the full pathway from DNA to protein to reaction: a gene must be transcribed into mRNA, translated into a polypeptide, folded into a functional enzyme, and only then can it catalyze a metabolic reaction. This framework allows researchers to ask deeper questions about proteome allocation, resource bottlenecks, stress responses, and evolutionary trade-offs.
ME-models are constructed by combining:
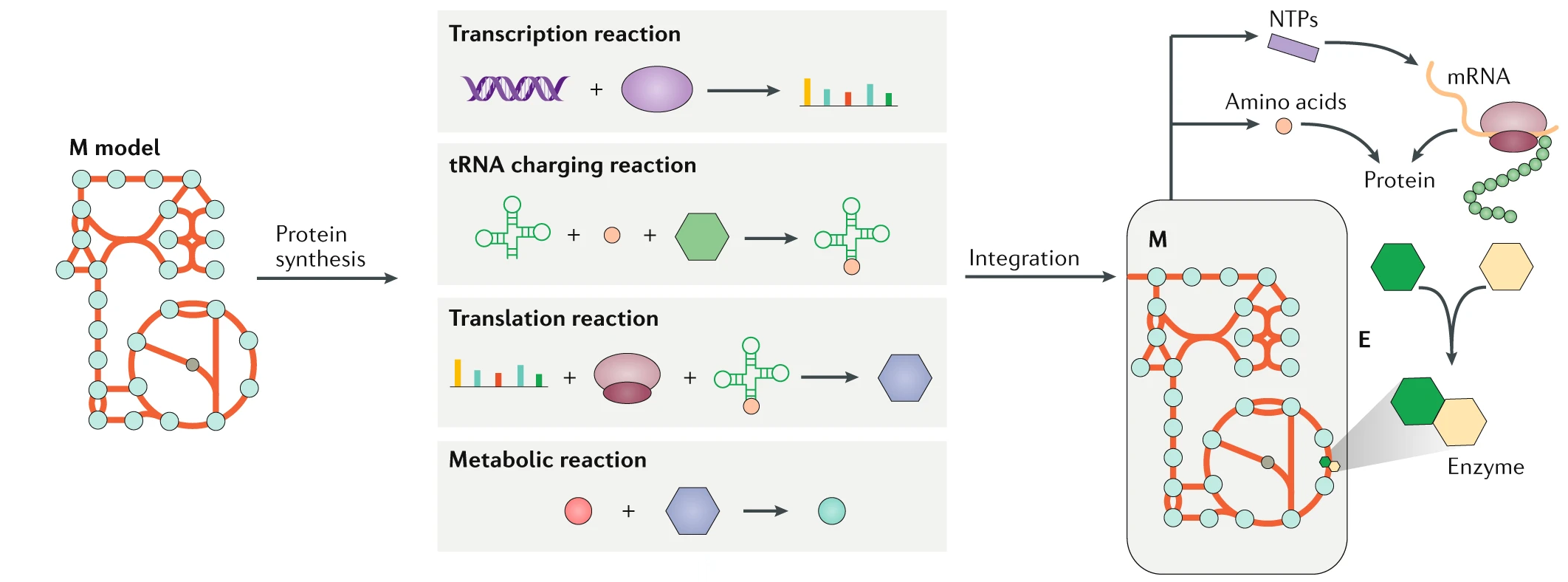
Figure: The M-model simulates metabolism. ME-models integrate additional layers including transcription, tRNA charging, translation, and protein complex formation. These processes are merged into a single stoichiometric system that balances metabolic function with gene expression.
The ME-modeling framework emerged from decades of model development in the Palsson Lab and the systems biology community. As shown below, the field has evolved from simple metabolic reconstructions to multi-layered models capable of simulating transcriptional regulation, stress adaptation, and protein resource allocation.
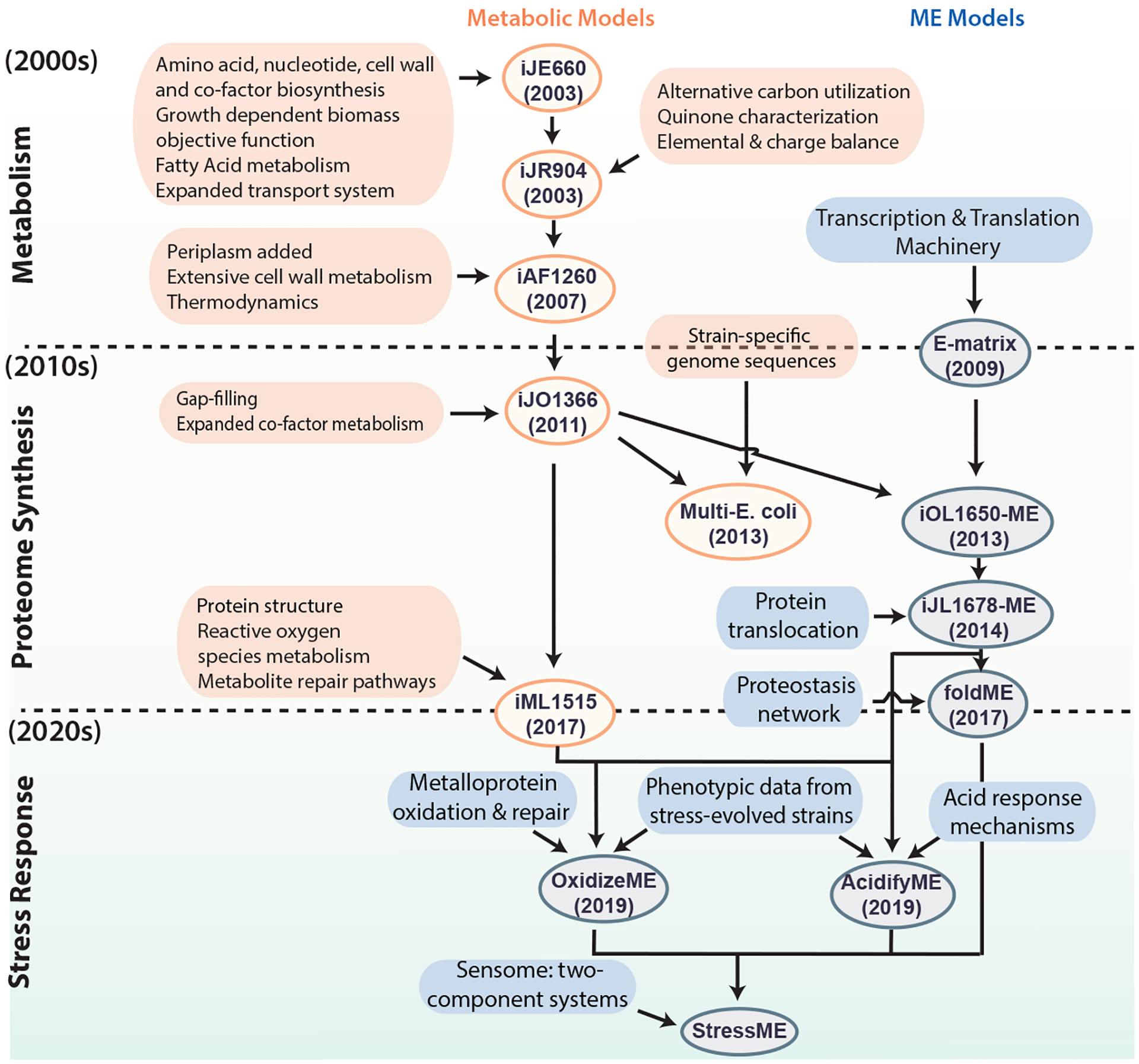
Figure: Timeline of E. coli genome-scale model development. Metabolic models grew in scope during the 2000s. By the 2010s, gene expression pathways were added, enabling the first ME-models. In the 2020s, ME-models have expanded to include stress response mechanisms such as temperature (FoldME), oxidative stress (OxidizeME), and acid stress (AcidifyME).
By integrating gene expression and resource constraints, ME-models bring us closer to a complete, mechanistic model of a living cell. This enables more predictive simulations, improved data integration, and deeper biological discovery than ever before.
Biological systems are deeply interconnected, and genome-scale models aim to capture that complexity. Simulating a single cell like E. coli at this level of detail involves thousands of reactions, genes, and molecular interactions, all subject to physical, chemical, and biological constraints. ME-models are especially challenging because they do not just simulate metabolism; they also simulate how the cellular machinery that drives metabolism is constructed in the first place.
A single simulation requires accounting for:
keff)This creates a system that is nonlinear, highly constrained, and sensitive to missing data, which makes the modeling both powerful and computationally intensive.
Solving a ME-model isn't like solving a simple linear flux balance problem. These models are:
qMINOS or SoPlex)This complexity is exactly why we built this platform. It allows researchers to interact with ME-models more easily, without needing to configure specialized solver environments and coding packages locally from scratch.
This web app is designed for rapid exploration, visualization, and constraint testing. More advanced workflows, such as time-course simulations, stress-specific model variants, or fine-tuned optimization with custom solvers, can be performed locally using the published COBRAme and solveMEpy GitHub repositories.
Genome-scale models rely on constraints to make useful predictions. These constraints reduce the space of all mathematically possible cellular states to only those that are biochemically and physiologically feasible.

Figure: The solution space is shaped by constraints. Mass balance and flux bounds shrink the space of allowable solutions. Optimization of an objective function, such as biomass production, identifies the most likely cellular state.
In ME-models, constraints go far beyond mass balance and flux bounds. These models explicitly simulate the production and usage of enzymes through gene expression, which introduces a completely new dimension: the cost of gene expression or the cell’s proteome budget.
Because ME-models are large and nonlinear, they are solved in two steps:
μ) by testing increasing values and checking whether the entire system, including expression, is supportable.μ guess, the model maximizes production of a nonfunctional protein complex. This acts as a proxy for minimizing proteome usage, enforcing efficient resource allocation and enabling simulations of both batch and chemostat behavior.This structure yields both the maximum growth rate and the gene expression profile that supports it.
In laboratory-evolved strains, cells may operate close to optimal growth, making unconstrained ME-model predictions reasonably accurate. But wild-type strains do not. These strains often express genes involved in stress response, environmental sensing, or transport/catabolism of unused nutrients for bet-hedging.
Without omics-based constraints, ME-models will overpredict growth and underestimate unused proteome. To simulate strain-specific behavior accurately, additional constraints are required:
μ is known, enabling chemostat-like or condition-specific simulations.This is essential when reconstructing strain-specific ME-models from isolates, clinical samples, or time-course datasets.
This web app allows users to:
This platform makes it easier to apply experimental data and simulate realistic strain behavior, helping researchers translate complex biological constraints into meaningful, mechanistic predictions— all without needing to configure advanced solver environments.